高等数学学习笔记
第一章 极限与连续
1.1 函数
1.1.1 基本概念
函数: 定义域内总有唯一的y对应x
复合函数: 设$u=φ(x)(x∈D_1)$,$y=f(u)(u∈D_2)$,对于任意$x∈D_1$,有$φ(x)∈D_2$,则y为x的复合函数,记作$y=f(φ(x))$
反函数: 设$y=f(x)$为单调函数,$x∈D$,$y∈R$,若对于任意$y∈R$,有唯一的$x∈D$,使得$f(x)=y$,则称x是y的反函数,记作$x=f^{-1}(y)$
基本初等函数:
- 幂函数: $y=x^a(a∈R)$
- 指数函数: $y=a^x(a>0,a≠1)$
- 对数函数: $y=log_a x(a>0,a≠1)$
- 三角函数: $y=sin x,y=cos x,y=tan x,y=cot x,y=sec x,y=csc x$
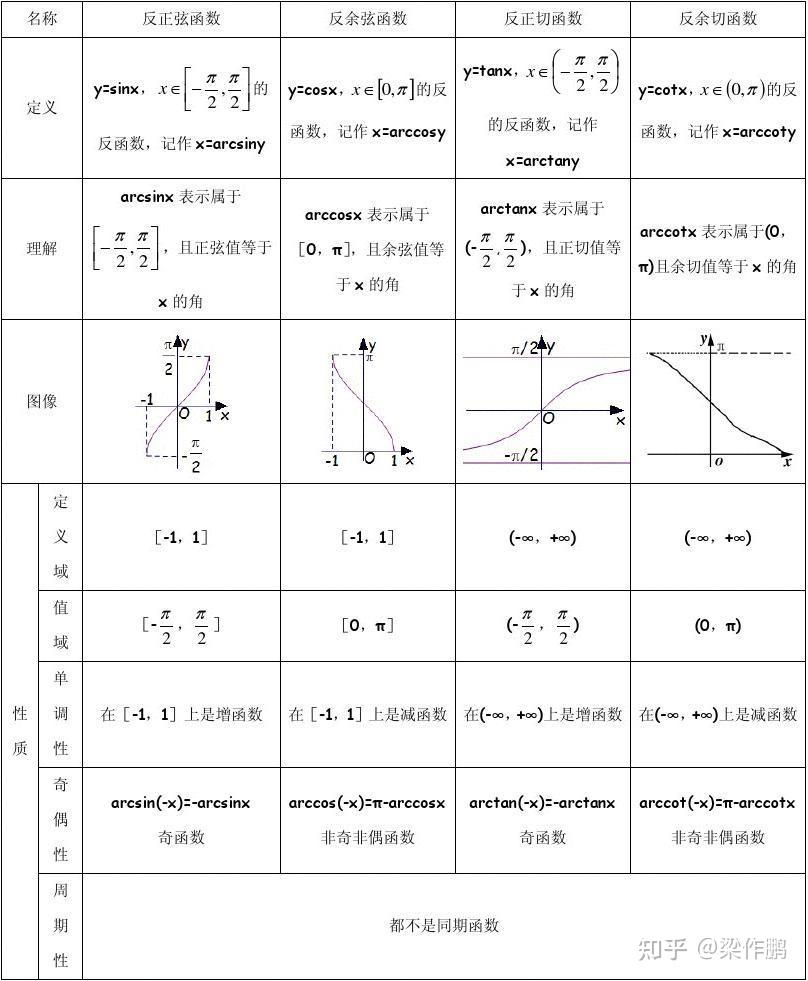
- 反三角函数: $y=arcsin x,y=arccos x,y=arctan x,y=arccot x,y=arcsec x,y=arccsc x$
三角函数复习
- 三角函数图象和性质
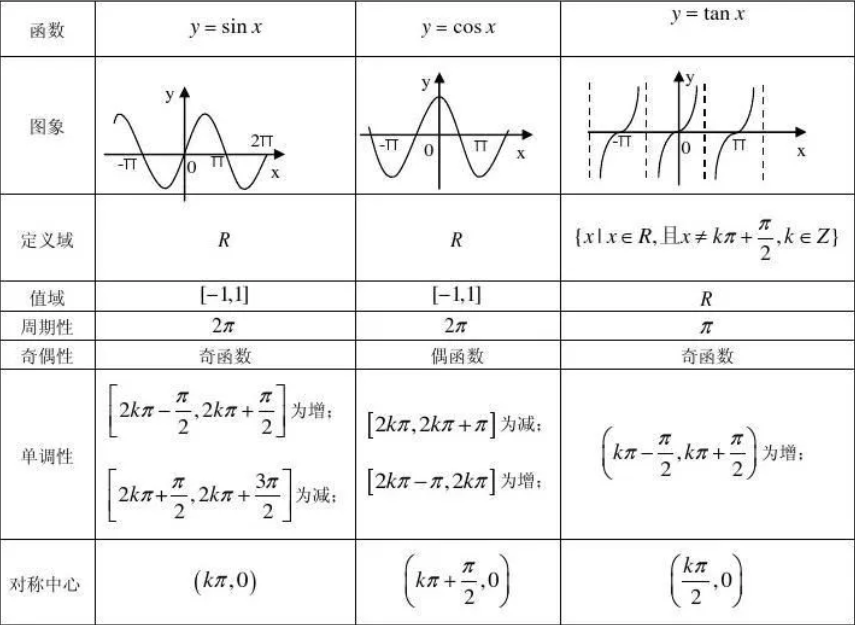
| 函数 | $y=cotx$ | $y=secx$ | $y=cscx$ |
|---|---|---|---|
| 图象 | 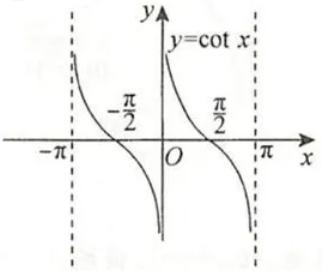 | 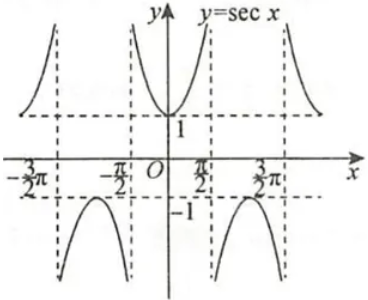 | 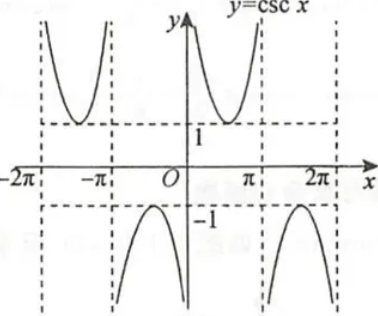 |
| 定义域 | $x≠kπ(k∈Z)$ | $x≠\frac{π}{2}+kπ(k∈Z)$ | $x≠kπ(k∈Z)$ |
| 值域 | $(-∞,∞)$ | $(-∞,-1]∪[1,∞)$ | $(-∞,-1]∪[1,∞)$ |
| 周期性 | $π$ | $2π$ | $2π$ |
| 奇偶性 | 奇函数 | 偶函数 | 奇函数 |
| 单调性 | $(kπ,kπ+π)$为减 | $[2kπ,2kπ+\frac{π}{2})∪(2kπ+\frac{π}{2})$为增,$(2kπ+π,2kπ+\frac{3π}{2})∪[2kπ+\frac{3π}{2},2π+2kπ)$为减 | $[2kπ+\frac{π}{2},2kπ+π)∪(2kπ+π,2kπ+\frac{3π}{2})$为增,$[2kπ-\frac{π}{2},2kπ)∪(2kπ,\frac{π}{2}+2kπ)$为减 |
| 对称中心 | $(\frac{kπ}{2},0)$ | $(\frac{π}{2}+kπ,0)$ | $(kπ,0)$ |
- 三角函数公式
基本公式
- $sec^2x=tan^2x+1$
- $csc^2x=cot^2x+1$
- $sin^2x+cos^2x=1$
- $tanx=\frac{sinx}{cosx}$
- $cotx=\frac{cosx}{sinx}$
- $secx=\frac{1}{cosx}$
- $cscx=\frac{1}{sinx}$
- $sinx+cosx=√2sin(x+\frac{π}{4})$
- $sinx-cosx=√2sin(x-\frac{π}{4})$
诱导公式
| 角\函数 | sin | cos | tan | cot |
|---|---|---|---|---|
| -x | -sinx | cosx | -tanx | -cotx |
| $\frac{π}{2}-x$ | cosx | sinx | cotx | tanx |
| $\frac{π}{2}+x$ | cosx | -sinx | -cotx | -tanx |
| π-x | sinx | -cosx | -tanx | -cotx |
| π+x | -sinx | -cosx | cotx | tanx |
| $\frac{3π}{2}-x$ | -cosx | -sinx | cotx | tanx |
| $\frac{3π}{2}+x$ | -cosx | sinx | -cotx | -tanx |
| 2π-x | -sinx | cosx | -tanx | -cotx |
| 2π+x | sinx | cosx | tanx | cotx |
- $sin(π±t)=∓sint$
- $cos(π±t)=-cost$
- $sin(\frac{π}{2}±t)=cost$
- $cos(\frac{π}{2}±t)=∓sint$
降幂公式
- $sin^2x=\frac{1-cos2x}{2}$
- $cos^2x=\frac{1+cos2x}{2}$
- $tan^2x=\frac{1-cos2x}{1+cos2x}$
倍角公式
- $sin2x=2sinxcosx$
- $cos2x=cos^2x-sin^2x=2cos^2x-1=1-2sin^2x$
- $tan2x=\frac{2tanx}{1-tan^2x}$
- $tan\frac{x}{2}=\frac{sinx}{1+cosx}=\frac{1-cosx}{sinx}=cscx-cotx$
和差公式
- $sin(x±y)=sinxcosy±cosxsiny$
- $cos(x±y)=cosxcosy∓sinxsiny$
- $tan(x±y)=\frac{tanx±tany}{1∓tanxtany}$
- $cot(x±y)=\frac{cotxcoty∓1}{coty±cotx}$
和差化积公式
- $sin\alpha+sin\beta=2sin(\frac{\alpha+\beta}{2})cos(\frac{\alpha-\beta}{2})$
- $sin\alpha-sin\beta=2cos(\frac{\alpha+\beta}{2})sin(\frac{\alpha-\beta}{2})$
- $cos\alpha+cos\beta=2cos(\frac{\alpha+\beta}{2})cos(\frac{\alpha-\beta}{2})$
- $cos\alpha-cos\beta=-2sin(\frac{\alpha+\beta}{2})sin(\frac{\alpha-\beta}{2})$
积化和差公式
- $sin\alpha sin\beta=\frac{1}{2}[cos(\alpha-\beta)-cos(\alpha+\beta)]$
- $cos\alpha cos\beta=\frac{1}{2}[cos(\alpha-\beta)+cos(\alpha+\beta)]$
- $sin\alpha cos\beta=\frac{1}{2}[sin(\alpha+\beta)+sin(\alpha-\beta)]$
万能公式
- $sinx=\frac{2tan\frac{x}{2}}{1+tan^2\frac{x}{2}}$
- $cosx=\frac{1-tan^2\frac{x}{2}}{1+tan^2\frac{x}{2}}$
- $tanx=\frac{2tan\frac{x}{2}}{1-tan^2\frac{x}{2}}$
常见不等式与数列
- 常见不等式
- 三角不等式:
- $||a|-|b||≤|a±b|≤|a|+|b|$
- 算数不等式:
- $a^2+b^2≥2ab$
- $|ab|≤\frac{a^2+b^2}{2}$
- a≥0时:
- $\frac{a_1+a_2+…+a_n}{n}≥^n√{a_1a_2…a_n}$
- 柯西不等式:
- $(a_1^2+a_2^2+…+a_n^2)(b_1^2+b_2^2+…+b_n^2)≥(a_1b_1+a_2b_2+…+a_nb_n)^2$
- 常见数列

函数的初等特性
- 有界性: 设$y=f(x)$,若存在常数M>0,使得对于定义域D内的任意x,有$|f(x)|≤M$,则称f(x)在D上有界
- 有界的充分必要条件是函数的值域有上界和下界
单调性:设$y=f(x)$,若对于定义域D内的任意$x_1,x_2$,当$x_1 < x_2$时,有$f(x_1) < f(x_2)$,则称f(x)在D上单调递增;若对于定义域D内的任意$x_1,x_2$,当$x_1 < x_2$时,有$f(x_1) > f(x_2)$,则称f(x)在D上单调递减
奇偶性:设$y=f(x)$,定义域D关于原点对称,若对于定义域D内的任意x,有$f(-x)=-f(x)$,则称f(x)为奇函数;若对于定义域D内的任意x,有$f(-x)=f(x)$,则称f(x)为偶函数
周期性:设$y=f(x)$,若存在常数T>0,使得对于定义域D内的任意x和$x±T$,有$f(x)=f(x±T)$,则称f(x)为周期函数,T为函数f(x)的周期
1.2 极限
1.2.1 极限的定义
极限

- x → a :x趋于a,不能等于a,且从左右两侧趋近
- $lim_{x→a}f(x)与f(a)$无关
- 0<|x-a|<δ是一个去心邻域
- |f(x)-A|<ε就是ε可以要取多小就取多小,要多接近A就有多接近A
左极限 右极限
若对任意的$ε>0$,存在$δ>0$,使得当$x∈(a-δ,a)$时,有$|f(x)-A|<ε$,则称A为f(x)在x=a的左极限,记作$f(a-0)$
若对任意的$ε>0$,存在$δ>0$,使得当$x∈(a,a+δ)$时,有$|f(x)-B|<ε$,则称B为f(x)在x=a的右极限,记作$f(a+0)$
- $lim_{x→a}f(x)=A$的充分必要条件是$f(a-0)=f(a+0)=A$
- 对于$lim_{x→b}f(x)$,若表达式中含有$a^{\frac{h(x)}{x-b}}$或$a^{\frac{h(x)}{b-x}}$时,一定要讨论左、右极限
- 对于$lim_{x→a}arctan\frac{1}{x-a}$时,一定要讨论左、右极限
无穷小
若$lim_{x→a}f(x)=0$,则称f(x)是x→a时的无穷小
设$f(a)→0$,$f(b)→0$
- 若$lim\frac{f(b)}{f(a)}=0$,则称f(b)是f(a)的高阶无穷小,记作$f(b)=o(f(a))$
- 若$lim\frac{f(b)}{f(a)}=k(k≠0,∞)$,则称f(b)是f(a)的同阶无穷小,记作$f(b)=O(f(a))$
- 特别地,若$lim\frac{f(b)}{f(a)}=1$,则称f(b)是f(a)的等价无穷小,记作$f(a)∼f(b)$
无穷小的性质
- 一般性质:
- 0是与自变量趋向无关的无穷小
- $f(x)=3(x-1)^2$,当$x→1$时为无穷小,当$x→a(a≠1)$时不是无穷小
- 有限个无穷小的和差是无穷小
- 有界函数或常数与无穷小的乘积是无穷小
- 无穷大:若$lim_{x→a}\frac{1}{f(x)}=0$,则称f(x)是x→a时的无穷大
- 等价性质:
- a
a_1,bb_1,且$lim\frac{b_1}{a_1}=A$,则$lim\frac{b}{a}=A$
- a
- 常见等价无穷小:
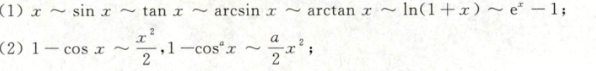
1.2.2 极限的性质
一般性质
唯一性若极限存在,则极限一定唯一
- 证明:

- 典型例题:
保号性设$lim_{x→a}f(x)=A>0(A<0),则存在$δ>0$,使得当$0<|x-a|<δ$时,有$f(x)>0(f(x)<0)$
- 证明:
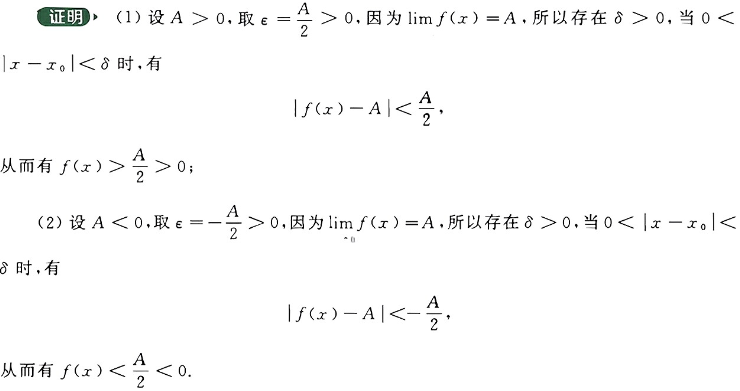
- 典型例题:
$f’(x)=0,lim_{x→a}\frac{f’(x)}{(x-1)^3}=-2,问x=1是极值点吗?$ 解: $\because lim_{x→a}\frac{f’(x)}{(x-1)^3}=-2$ $\therefore \exists \delta>0,当0<|x-1|<\delta时,\frac{f’(x)}{(x-1)^3}<0$ $$ \begin{cases} f’(x)>0 & , x \in (1-\delta,1) \ f’(x)<0 & , x \in (1,1+\delta) \end{cases} $$ $ \therefore x=1是f(x)的极大值 $
有界性
数列极限的有界性 若数列极限存在,则数列必有界,反之不成立
函数极限的局部有界性 若$lim_{x→a}f(x)=A$,则存在$\delta$>0,M>0,使得当$0<|x-a|<\delta$时,有$|f(x)|<M$
证明: 取$ε=1$,则存在$δ>0$,使得当$0<|x-a|<δ$时,有$|f(x)-A|<1$,则$|f(x)|<|A|+1$,(||f(x)|-|A||≤|f(x)-A|<1) 取$M=|A|+1$,则有$|f(x)|≤M$
- ε是极限定义中的任意小正数
典型例题:
数列极限与子列极限的关系
若数列有极限,则数列的任意子列都有相同的极限 若某一子列有极限,则该数列不一定有极限
存在性质
夹逼定理(迫敛定理)
$$ 设 \begin{cases} f(x)≤g(x)≤h(x) , \ limf(x)=limh(x)=A , \end{cases} 则limg(x)=A $$
证明:
典型例题:
次数不齐可能用夹逼定理
- 存在数列,求$lim_{n→∞}\frac{n^2}{2^n}$? 解: $ n充分大时,2^n=(1+1)^n=C^{0}{n}+C^{1}{n}+…+C^{n}{n}≥C^{3}{n}=\frac{n(n-1)(n-2)}{6}$ $ \therefore 0<\frac{n^2}{2^n}≤\frac{6n^2}{n(n-1)(n-2)}$ $ \because lim_{n→∞}\frac{6n^2}{n(n-1)(n-2)},lim_{n→∞}0=0$ $ \therefore lim_{n→∞}\frac{n^2}{2^n}=0$
- $f(x)=lim_{n→∞}\sqrt[n]{x^n+x^{2n}}(x>0)$,求f(x)? x可以看作正常数,n是变量 解: $当0<x≤1时,x^n≤x^n+x^{2n}≤2x^{n}$ $ \therefore x≤\sqrt[n]{x^n+x^{2n}}≤2^{\frac{1}{n}}x$ $ \because lim_{n→∞}x=lim_{n→∞}2^{\frac{1}{n}}x=x$ $ \therefore lim_{n→∞}\sqrt[n]{x^n+x^{2n}}=x$ $ 当x>1时,x^{2n}≤x^n+x^{2n}≤2x^{2n}$ $ \therefore x^2≤\sqrt[n]{x^n+x^{2n}}≤2^{\frac{1}{n}}x^2$ $ \because lim_{n→∞}x^2=lim_{n→∞}2^{\frac{1}{n}}x^2=x^2$ $ \therefore lim_{n→∞}\sqrt[n]{x^n+x^{2n}}=x^2$ $$ 综上所述, \begin{cases} x & , 0<x≤1 \ x^2 & , x>1 \end{cases} $$
- $求lim_{n→∞}(\frac{1}{\sqrt{n^2+1}}+\frac{1}{\sqrt{n^2+2}}+…+\frac{1}{\sqrt{n^2+n}})$ 解: $ \frac{n}{\sqrt{n^2+n}}<\frac{1}{\sqrt{n^2+1}}+\frac{1}{\sqrt{n^2+2}}+…+\frac{1}{\sqrt{n^2+n}}<\frac{n}{\sqrt{n^2+1}}$ $ \because lim_{n→∞}\frac{n}{\sqrt{n^2+n}}=lim_{n→∞}\frac{1}{\sqrt{1+\frac{1}{n}}}=1$,同理$lim_{n→∞}\frac{n}{\sqrt{n^2+1}}=1$ $ \therefore lim_{n→∞}(\frac{1}{\sqrt{n^2+1}}+\frac{1}{\sqrt{n^2+2}}+…+\frac{1}{\sqrt{n^2+n}})=1$
单调有界定理单调有界的数列必有极限
证明:不用证明,记着就行
典型例题:
- note:
- ${a_n}有界⇔a_n有上界,有下界$
- ${a_n}单调递增$
- case 1:${a_n}无上界$ $⇒lim_{n→∞}a_n=+∞$
- case 2:$\exists M_0,a_n≤M_0$ $⇒lim_{n→∞}a_n \exists$
- ${a_n}单调递减$
- case 1:${a_n}无下界$ $⇒lim_{n→∞}a_n=-∞$
- case 2:$\exists m_0,a_n≥m_0$ $⇒lim_{n→∞}a_n \exists$
- 重要不等式:
- $当x≥0时,sinx≤x$
- $当x≥-1时,ln(1+x)≤x$
- $当x>0时,e^x≥1+x$
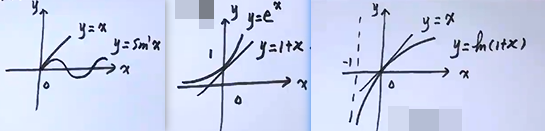
- 小结论:
- 设a,b,c>0则$lim_{n→∞}(a^n+b^n+c^n)^{\frac{1}{n}}=max(a,b,c)$
1.2.3 重要极限
$lim_{\triangle→0}\frac{sin\triangle}{\triangle}=1$
$lim_{\triangle→0}(1+\triangle)^{\frac{1}{\triangle}}=e$
$0<a<\pi/2时,sina<α<tana$
1.2.4 极限的运算法则
四则运算法则
- 设$lim_{x→a}f(x)=A,lim_{x→a}g(x)=B$,则:
- $lim_{x→a}[f(x)±g(x)]=A±B$
- $lim_{x→a}[f(x)·g(x)]=A·B$
- $lim_{x→a}\frac{f(x)}{g(x)}=\frac{A}{B}(B≠0)$
复合函数的极限
- 设$lim_{u→a}f(u)=A,lim_{x→x_0}g(x)=a$,且$g(x)≠a$,则:$lim_{x→x_0}f[g(x)]=A$
- 设$lim_{u→a}f(u)=f(a),lim_{x→x_0}g(x)=a$,则:$lim_{x→x_0}f[g(x)]=f(a)$
1.2.5 points
- 极限趋于∞,则不属于存在极限
1.3 连续与间断
1.3.1 连续与间断的定义
连续
- case 1: $f(x)$在$x=a$连续 如果$lim_{x→a}f(x)=f(a)$或$f(a-0)=f(a+0)=f(a)$,则称f(x)在x=a连续
- 如果 f(a+0)=f(a),则称f(x)在x=a右连续
- 如果 f(a-0)=f(a),则称f(x)在x=a左连续
- case 2: $f(x)$在$[a,b]$连续: 若满足:
- f(x)在(a,b)上任意一点连续
- f(a)=f(a+0)
- f(b)=f(b-0) 则称f(x)在$[a,b]$连续,记作$f(x)∈C[a,b]$
间断
若$f(a)≠lim_{x→a}f(x)$,则称f(x)在x=a处不连续,x=a称为间断点
间断点的分类:
- 第一类间断点: $f(a-0),f(a+0)$存在,其中:
- 1 $f(a-0)=f(a+0)≠f(a)$,称为可去间断点
- 2 $f(a-0)≠f(a+0)$,称为跳跃间断点
- 第二类间断点: $f(a-0),f(a+0)$至少有一个不存在,其中:
- 1 $f(a-0),f(a+0)$至少有一个为无穷大,称为无穷间断点
典型例题:
- $f(x)=\frac{x^{\frac{1}{x}}}{1+2^{\frac{1}{x}}}·\frac{x^2+x-2}{x^2-1}$ 解: $f(x)=\frac{x^{\frac{1}{x}}}{1+2^{\frac{1}{x}}}·\frac{x^2+x-2}{x^2-1}=\frac{x^{\frac{1}{x}}(x+2)(x-1)}{(1+2^{\frac{1}{x}})(x+1)(x-1)}$ $\therefore x=0,x=1, x=-1为间断点$ $\because lim_{x→-1}f(x)=∞$ $\therefore x=-1为第二类间断点$ $\because f(0-0)=0 ≠ f(0+0)=2$ $\therefore x=0 为 跳跃间断点$ $\because lim_{x→1}f(x)=1$ $\therefore x=1 为 可去间断点$
1.3.2 闭区间上连续函数的性质
最值定理: 若f(x)在闭区间[a,b]上连续,则f(x)在[a,b]上有最大值和最小值有界定理: 若f(x)在闭区间[a,b]上连续,则f(x)在[a,b]上有界零点定理: 若f(x)在闭区间[a,b]上连续,且$f(a)·f(b)<0$,则在(a,b)内至少有一点x_0,使得f(x_0)=0
- 如果题目中有$ifc\in (a,b)$,很可能使用零点定理
介值定理: 若f(x)在闭区间[a,b]上连续,对任意的$\eta\in [m,M],其中,m,M分别为f(x)在[a,b]上渠道的最小值和最大值,则存在\xi\in [a,b],使得f(\xi)=\eta$
如果题目中有$ifc\in [a,b]$或函数值之和,很可能使用零点定理
典型例题:

- $f(x)\in C[0,2],f(0)+2f(1)+3f(2)=12,求证: \exists\xi\in[0,2],f(\xi)=2$ 证:$\because f(x)\in C[0,2]$ $\therefore \exists m,M 6m≤f(0)+2f(1)+3f(2)≤6M$ $m≤2≤M$ $\therefore \exists \xi \in [0,2] ,使f(\xi)=2$ (介值定理)
积分中值定理$设f(x)\in C[a,b],证明\exists\xi\in[a,b],使得\int_{a}^{b}f(x)dx=f(\xi)(b-a)$ 证:$\because f(x)\in C[a,b]$ $\therefore \exists m,M$ $m≤f(x)≤M$ $\therefore \int_a^bmdx≤\int_a^bf(x)dx≤\int_a^bMdx$ $\therefore m(b-a)≤\int_a^bf(x)dx≤M(b-a)$ $\therefore m≤\frac{\int_a^bf(x)dx}{b-a}≤M$ $\therefore \exists \xi \in [a,b] ,使f(\xi)=\frac{\int_a^bf(x)dx}{b-a}$ $即\exists\xi\in[a,b],使得\int_{a}^{b}f(x)dx=f(\xi)(b-a)$ (介值定理)
1.4 重点题型
1.4.1 题型一 n项和的极限
- 先和后极限
$lim_{n→∞}(\frac{1}{13}+\frac{1}{35}+…+\frac{1}{(2n-1)(2n+1)})$ 解: $lim_{n→∞}(\frac{1}{13}+\frac{1}{35}+…+\frac{1}{(2n-1)(2n+1)})$ $=\frac{1}{2}lim_{n→∞}(\frac{1}{1}-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+…+\frac{1}{2n-1}-\frac{1}{2n+1})$ $=\frac{1}{2}(1-0)=\frac{1}{2}$
- 分子次数齐,分母次数齐,分母高一次
- 使用定积分重要结论
- $lim_{n→∞}\frac{1}{n}\sum_{i=1}^{n}f(\frac{i-1}{n})=lim_{n→∞}\frac{1}{n}\sum_{i=1}^{n}f(\frac{i}{n})=∫_0^1f(x)dx$
- $lim_{n→∞}(\frac{1}{n^2+1^2}+\frac{2}{n^2+2^2}+…+\frac{n}{n^2+n^2})$ 解: $原式=lim_{n→∞}\sum_{i=1}^{n}\frac{i}{n^2+i^2}$ $=\frac{1}{n}\sum_{i=1}^{n}\frac{\frac{i}{n}}{1+(\frac{i}{n})^2}$ $=∫_0^1\frac{x}{1+x^2}dx$ $=\frac{1}{2}∫_0^1\frac{d(1+x^2)}{1+x^2}$ $=\frac{1}{2}ln(1+x^2)|_0^1$ $=\frac{1}{2}ln2$
- $lim_{n→∞}(\frac{1}{\sqrt{n^2+1^2}}+\frac{1}{\sqrt{n^2+2^2}}+…+\frac{1}{\sqrt{n^2+n^2}})$ 解: $原式=lim_{n→∞}\sum_{i=1}^{n}\frac{1}{\sqrt{n^2+i^2}}$ $=lim_{n→∞}\frac{1}{n}\sum_{i=1}^{n}\frac{1}{\sqrt{1+(\frac{i}{n})^2}}$ $=∫_0^1\frac{dx}{\sqrt{1+x^2}}$ $=ln(x+\sqrt{1+x^2})|_0^1$ $=ln(1+\sqrt{2})$
- 分子或分母次数不齐,用夹逼定理
- $lim_{n→∞}(\frac{1^2}{n^3+1})+(\frac{2^2}{n^3+2})+…+(\frac{n^2}{n^3+n})$ $\frac{\frac{1}{6}n(n+1)(2n+1)}{n^3+n}≤原式≤\frac{\frac{1}{6}n(n+1)(2n+1)}{n^3+1}$ $lim_{n→∞}左式=lim_{n→∞}右式=\frac{1}{3}$(分子分母同时除以$n^3$) $∴原式=\frac{1}{3}$
1.4.2 题型二 不定型
- 例题见
25汤家凤高数辅导讲义.pdfp16
- $\frac{0}{0}$型
notes:

- $1^∞$型
notes:

- $\frac{∞}{∞}$型
notes:

- $0*∞$型
notes:
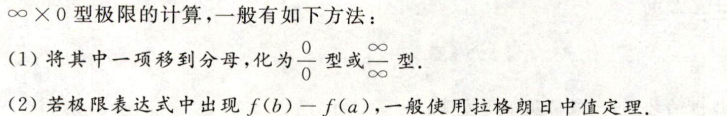
- $∞-∞$型
notes:

- $∞^0$型和$0^0$型
notes:$a^b->e^{lna^b}->e^{blna}$

1.4.3 题型三 证明数列存在极限
notes:


1.4.4 题型四 连续与间断
1.0 notes
!记录一下重要的等价无穷小、极限、什么时候可以用等价无穷小、极限四则运算
没事干试试分子分母同除以x,把x变成$\frac{1}{x}$
搞清楚定义!
第二章 导数与微分
2.1 导数和微分的基本概念
2.1.1 导数的定义
导数

- notes:


高阶导数

可微
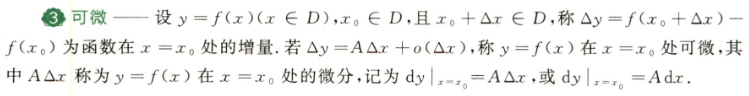
- notes:
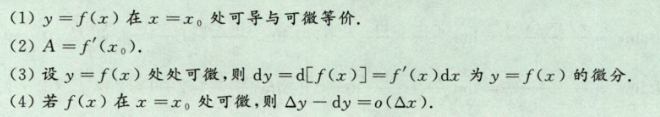
2.1.2 连续、可导、可微的关系
- 可导和可微等价
- 可导必连续,连续不一定可导
2.2 求导公式与法则
2.2.1 基本导数公式
- 幂函数、指数函数、对数函数、三角函数、反三角函数

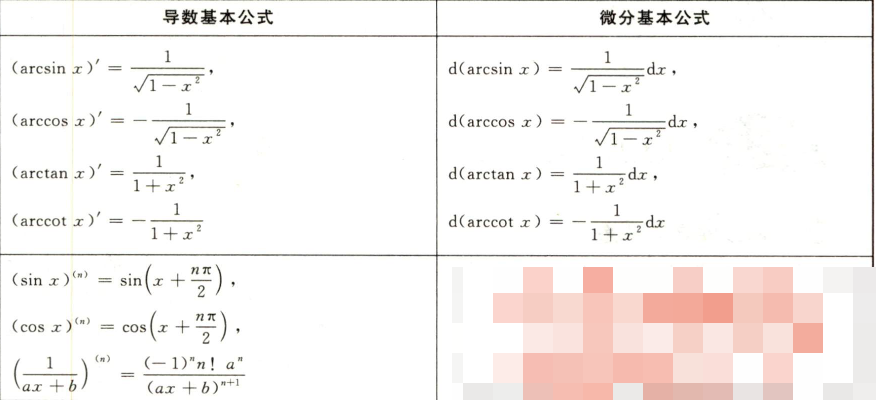
2.2.2 导数的四则运算

2.2.3 复合函数求导法则————链式法则
$设y=f(u),u=g(x)可导,且g’(x)≠0,则y=f[g(x)]可导,且\frac{dy}{dx}=\frac{dy}{du}·\frac{du}{dx}=f’(u)·g’(x)=f’[g(x)]·g’(x)$
2.2.4 反函数求导法则
- 反函数就是y=f(x)->x=g(y)。

2.3 隐函数与参数方程确定的函数求导
- 例题见
25汤家凤高数辅导讲义.pdfp45
2.3.1 隐函数的导数
隐函数

隐函数存在定理

2.3.2 参数方程确定的函数求导

- 例题:
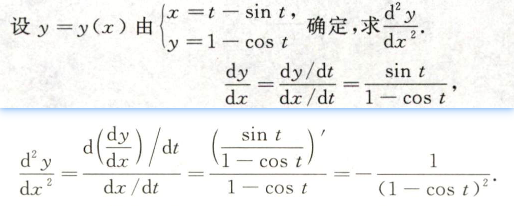
- notes:
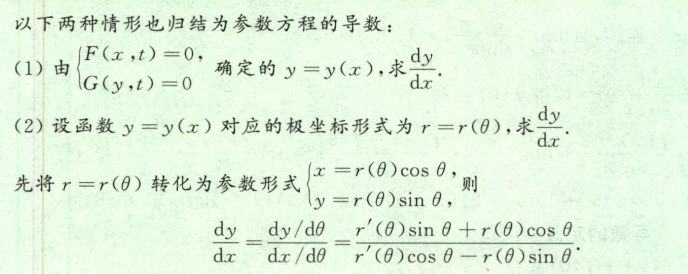
2.3.3 分段函数求导
连续性 $f(\Delta -0)=f(\Delta +0)=f(\Delta)$
x=a点存在极限,$f’{-}(a)=f’{+}(a)$
2.3.4 高阶导数

2.0 notes
- 多变出几个式子互相加减
- $\Delta _1 ^ {\Delta _2}$化成$e^{\Delta _2ln\Delta _1}$,如$(x+1)^{sinx}$化为$e^{sinxln(x+1)}$
- 形如$\sqrt{x^2+y^2}=arctan\frac{y}{x}$的隐函数求导,将y看作g{x} 求导为$\frac{2x+2yy’}{2\sqrt{x^2+y^2}}=\frac{1}{1+(\frac{y}{x})^2}*\frac{xy’-y}{x^2}$
第三章 一元函数微分学的应用
3.1 中值定理
3.1.1 预备知识
极值点:

f'(x)的几种情况:- 设f(x)在x=a处取极值,则f’(a)=0或f’(a)不存在,反之不成立
- 设f(x)可导且在x=a处取极值,则f’(a)=0
3.1.2 罗尔定理
f(x)∈C[a,b]————f(x)在[a,b]上连续

3.1.3 拉格朗日中值定理
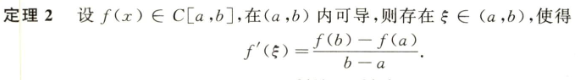


3.1.4 柯西中值定理
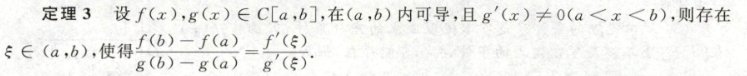
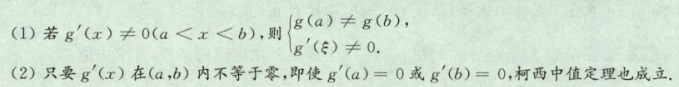
3.1.5 洛必达法则
- 法则一
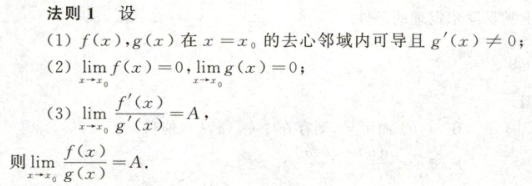
- 法则二

- notes
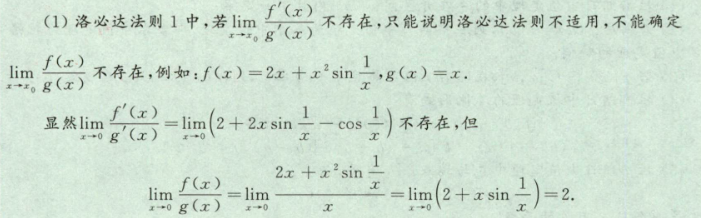
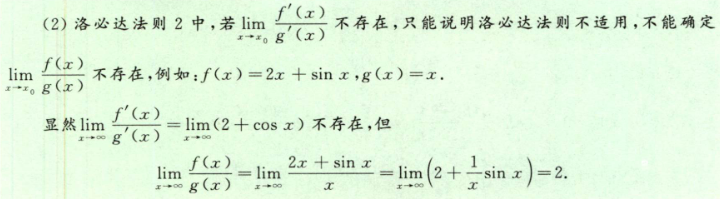
3.1.6 泰勒中值定理
- 定理一

- 定理二

- 麦克劳林公式
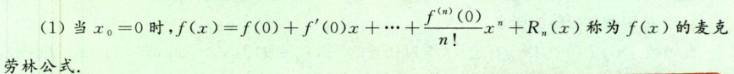
- 常见麦克劳林公式
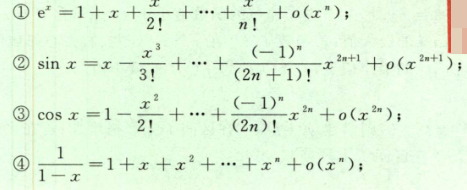
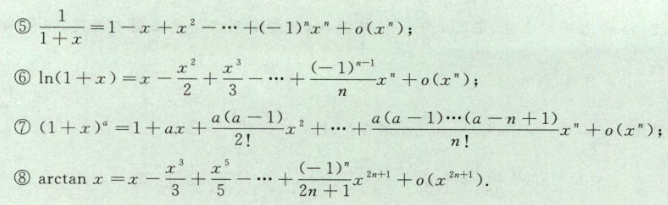
3.2 单调性与极值、凹凸性与拐点、函数作图
- 驻点: $f’(x)=0$的点
3.2.1 单调性


3.2.2 极值

极值判定法则:
确定定义域x∈D
求导数f’(x),求出驻点和不可导点
判别法:

3.2.3 凹凸性与拐点
- 凹凸性
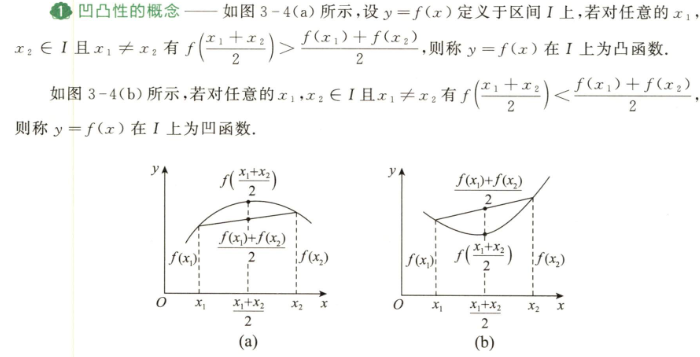
- 渐近线判别
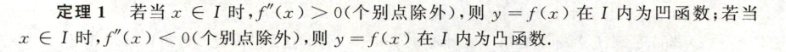
- 拐点

- 拐点判定
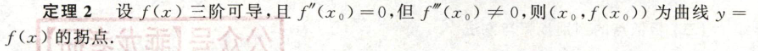
3.2.4 渐近线
- 水平渐近线
若$lim_{x→∞}f(x)=A$,则y=A是f(x)的水平渐近线
- 铅直渐近线
若$lim_{x→a}f(x)=∞$或$f(a-0)=∞或f(a+0)=∞$,则x=a是f(x)的铅直渐近线
- 斜渐近线
若$lim_{x→∞}\frac{f(x)}{x}=a(a≠0,a≠∞)$,$lim_{x→∞}[f(x)-ax]=b$,则y=ax+b是f(x)的斜渐近线
3.2.5 弧微分、曲率、曲率半径
- 弧微分(基本公式)
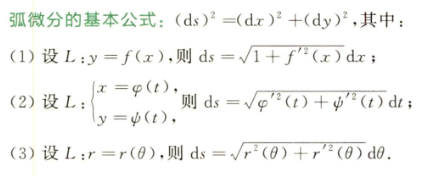
- 曲率与曲率半径
3.2.6 函数作图

3.2.7 重点题型
- 例题见
25汤家凤高数辅导讲义.pdfp62
Part 1 中值定理
题型一 证明$f^{(n)}(x)=0$
- notes:

题型二 待证明结论中只有一个$\xi$,不含其他字母
- case 1:
- 证明式子两项
- 导数相差一阶

$\frac{f’(x)}{f(x)}=(lnf(x))'$
$\frac{f’’(x)}{f’(x)}=(lnf’(x))'$
case 2:
- 证明式子多于两项
- 导数相差非一阶

题型三 待证明结论中含有$\xi和a、b$
- case 1: $a、b和\xi可分离$

- case 2: $a、b和\xi不可分离$

题型四 待证明结论中含有两个及以上中值
- case 1: $结论中只含有f’(\xi) f’(\eta)$

- case 2: $结论中含有两个中值项\xi \eta,但复杂度不同$

- case 3: $结论中含中值项\xi \eta,且完全对等$

题型五 待证明结论中含有$\theta$
题型六 拉格朗日定理用法

3.2.0 notes
- 要证明的式子,对着构造函数
- 研究构造什么函数的过程在草稿纸上,不用写在卷子上

